Morchella
Last year, I attended a mushroom course on how to learn to identify mushrooms, and it was a lot of fun and I learned a lot.
After the winter break, when spring was starting, I was wondering if I should try my luck with morels - why wait until fall to obsess over mushrooms again? :)
Where to start?
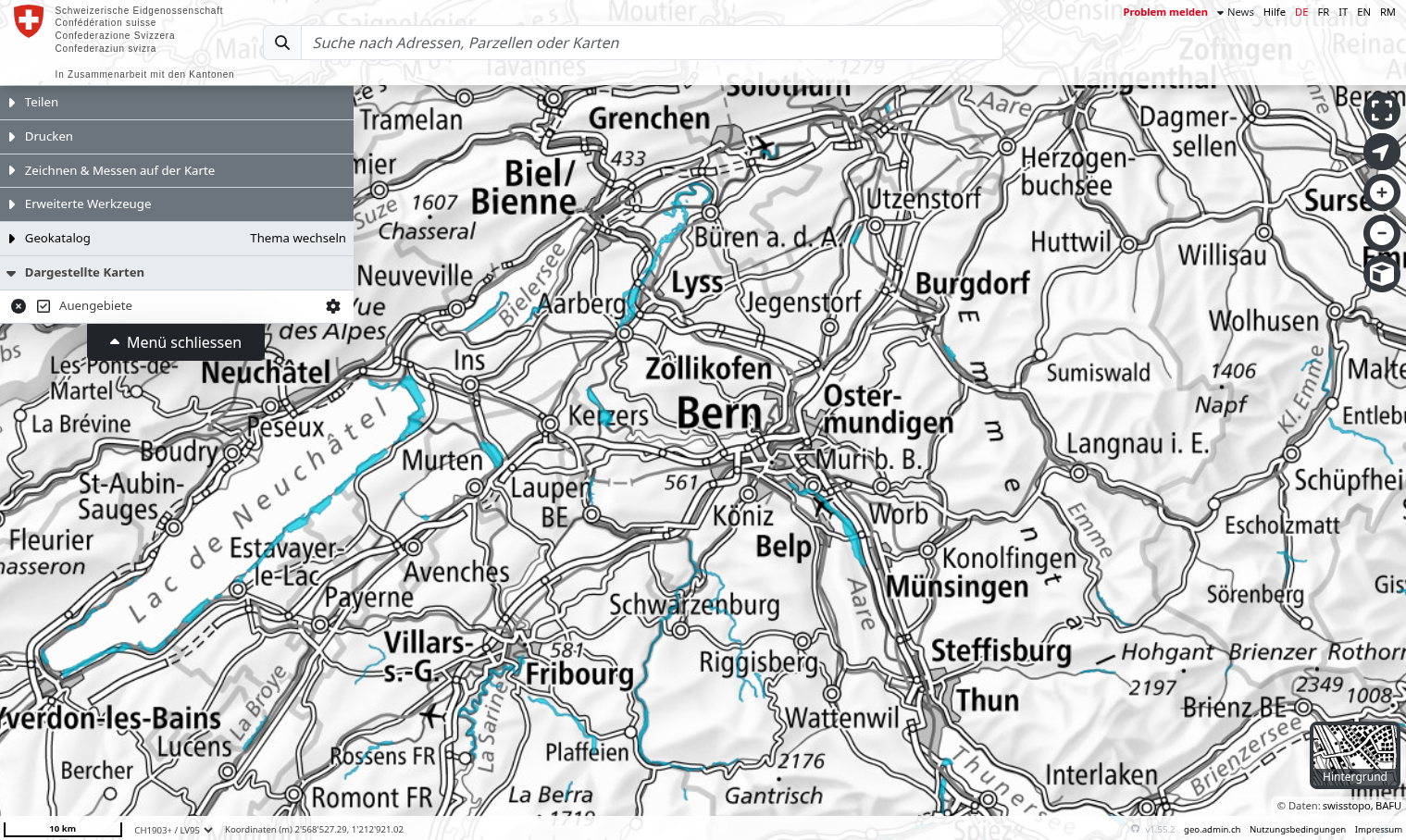
I started out on my own by reading where they should appear - it seems that "Auengebiete" (meadows, wetlands) have a good chance for morels. Luckily, the BAFU from the swiss government has a lot of data and maps. The Auengebiete can be shown as layer to see where there might be potential, marked in blue:
There would be also other layers like Waldmischungsgrad (percentage of deciduous trees) or Vernässung (water in the ground which doesn't come from precipitation). I shortly started looking into QGIS, but being a newbie with GIS-software then shortly stopped and looked for a different approach.
I asked some people who I knew had experience with finding morels, and got some valuable insights. Apparently morels can be notoriously hard to find, and also don't appear every year, if the conditions like weather and temperature are not matching.
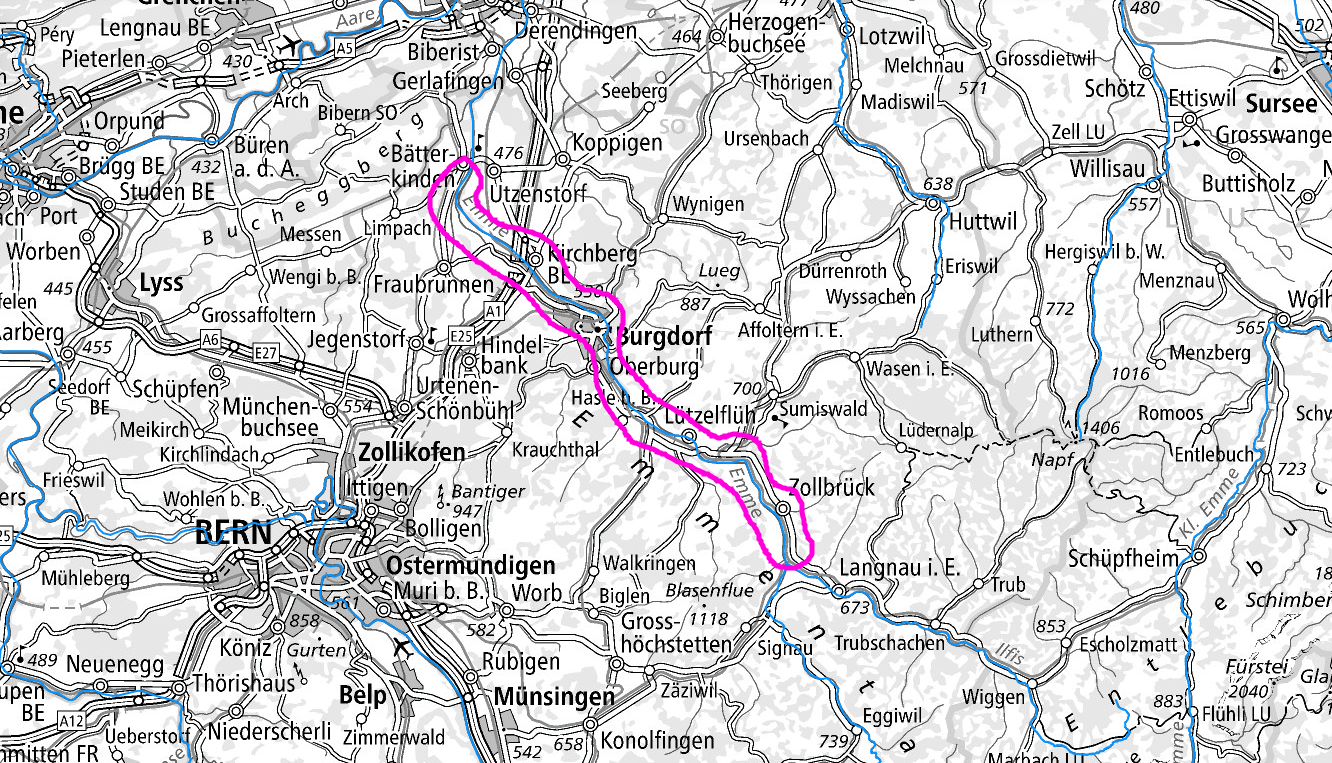
I got some good pointers for Auengebiete in my surroundings where morels have been found in the past. I mainly focussed on the region of the Emme around Burgdorf:
Trees and plants
An equally important part are the trees which the morels can have a symbiosis with - typically mentioned are Erle (Alnus), Esche (Fraxinus), Weide (Salix) and Pappel (Populus):

There are also other, less common combination, for example with the Ulme (Ulmus). As I understood, deciduous trees are what we are looking for in general.
Other plants can serve as indicator plants, so when you see those, the general conditions would be also suitable for morels.
Some examples are: Salomonssiegel (Polygonatum multiflorum):

Aronstab (Arum maculatum) and Buschwindröschen (Anemone nemorosa):


There are a lot of others, and I can recommend the book Morcheln: Ökologie und Lebensräume for a deep dive into the habitat of the different types of morels.
Weather
Another factor is the weather. Morels, like other mushrooms, are dependent on precipitation and temperature. So if it didn't rain for a long time, chances might be quite low to find anything.
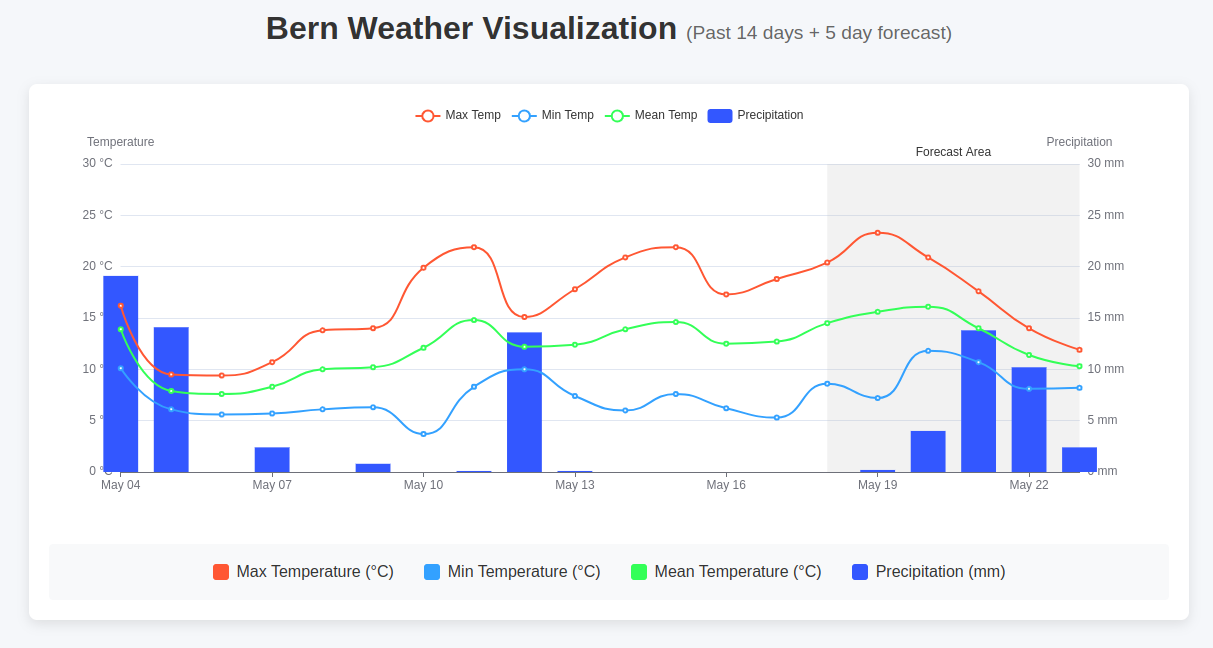
To have an overview tailored to my needs, I decided to create a small app using replit (with use of their AI agent) and the open-meteo.com API. The important bits are:
- 2 weeks of historical data, 5 days of forecast. This would allow to get a grasp of the current situation and the upcoming days.
- Precipitation and different temperature values: min, max and mean. Only the maximum temperature can be misleading and might not give enough information weather the ground was warm enough.
You can see the live version here: Weather dashboard.
Getting lucky
And after some trips, I did manage to get lucky and at least find a few morels. Here are two a nice specimen:


Over all it seemed to be too cold and too dry this year for morels, but maybe next year will be better...? At least I will be prepared :)
Good luck and happy morel hunting!