No Man’s Sky ship cost calculator

TLDR; Ever wondered how much a ship costs in No Man's Sky? Here's how much:
After playing No Man's Sky for some time, I noticed two things about ships and slots: First, the cost of the ships available always seems to be something random around a fixed value. For a 31 slots ship, sometimes the cost is around 11.6 million, sometimes 12.3 or even 12.5.
Second, the increase per additional slot (ratio slot-price) is not linear, but instead it seems to be some kind of exponential progress.
I wondered what the real relation is between price cost and slots, so I started to take some notes. You can have a look at the 72 data points here: 
(The cost is in million and rounded to a tenth of a million.)
Searching for a formula
At first, I thought the ratio from slots to price would exponential, something in the form like
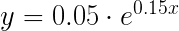
(y = cost of ship, x = amount of slots) But the line is too steep for the higher slots. After playing around a bit I realized that it would be more something like the following
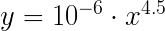
Here are both of the lines for comparison:
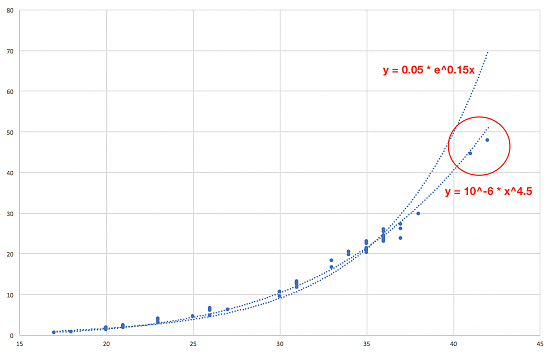
As you can see, the both rightmost points don't really fit the first equation, whereas the second equation is a much better fit. If we look closely at the middle part between 30 and 35 slots, there the second equation also is a slightly better fit.
Optimizing
To fiddle out the exact parameters, I wrote a simple python script to optimize the exponent:
def mse(factor):
return sum([(0.000001 * entry[0]**factor - entry[1])**2 for entry in data])/len(data)
with open('data.csv', 'r') as csv_file:
content = csv_file.readlines()
data = []
for line in content:
data.append([float(line.split(',')[0]), float(line.split(',')[1].strip())])
round = 0
factor = 1.0
diff = 1.0
best_mse = 1000
best_factor = 0
while round < 100:
factor += diff
print("MSE with ", factor, ":", mse(factor))
# if new best, remember current factor
if mse(factor) < best_mse:
best_mse = mse(factor)
best_factor = factor
else:
factor = best_factor
diff = diff/2
round += 1This gives the following output (to the left is the exponent, on the right the mean squared error):
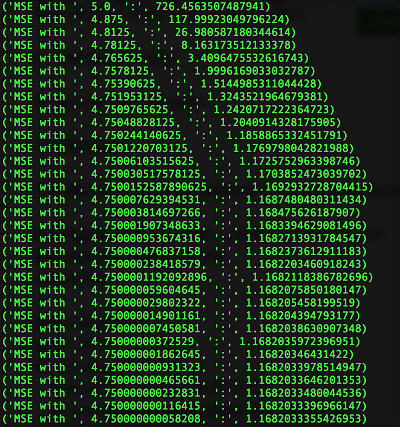
Bingo! So the formula (price in million) is:
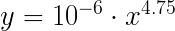
Or in other words, for the full price, the formula is really simple:
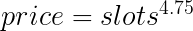
Calculating mining time
As you can see above I also included an approximate mining time, which is based on an optimistic mining rate, for one of those planets which is full of gold piles.
For a full slot of gold, 250 units, I used 2 minutes and 30 seconds. A full slot of gold gives 55'000 units of gold, so that's 22'000 units per minute.
Happy mining! :-)