kleemans.ch

Some months back I stumbled across this revealing blog post from Silviu Tantos from iconfinder.com. It's about how to compare two images and to quantify the difference into a single number, showing how much an image looks like another image.

For example: How much do these two images, a surprised koala and the same image but only with a fancy red hat, really look like one another? 80%? 90%? More?

And how yould you calculate such a difference without having to iterate over all the pixels?

I remember being intrigued back then when Google released its 'search by image' feature, by which I was equally impressed at the time. How was it possible to determine (with such accuracy!) if two images "look" like each other, or even to search for them?

The simple idea behind the whole algorithm described in the post really is fascinating and made it feel like being handed a well-kept secret :-) So I'd like to share some aspects of it accompanied by a simple Python script.

Scaling and removing colors

First of all, we want to compare all sorts of images, so also all kind of sizes. So we have to scale them down to a common size. If we choose a small size, calculation will be easier later on. For example 9x8 pixels (an uneven number in the linesize to make the dhash function work, see below).

Our two koalas will look like follows (enlarged for better visibility):

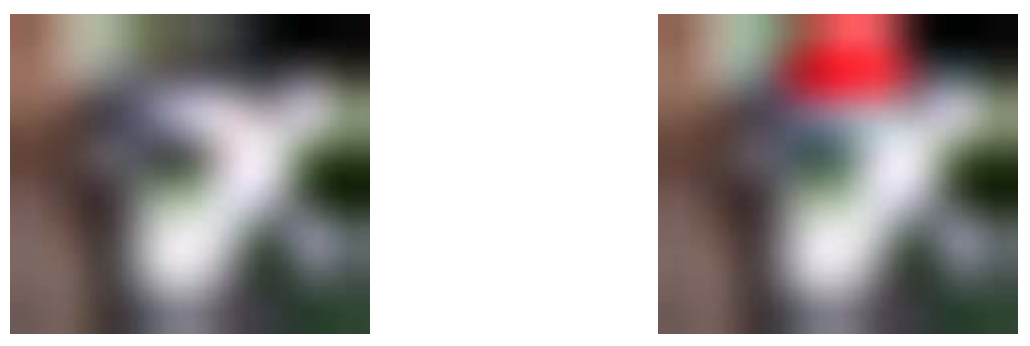
And after greyscaling, only the "intensity values" will stay, the R-G-B triplet will be reduced to one simple value. Technically, this step is done before, but for illustrating its effect, here is it now :-):

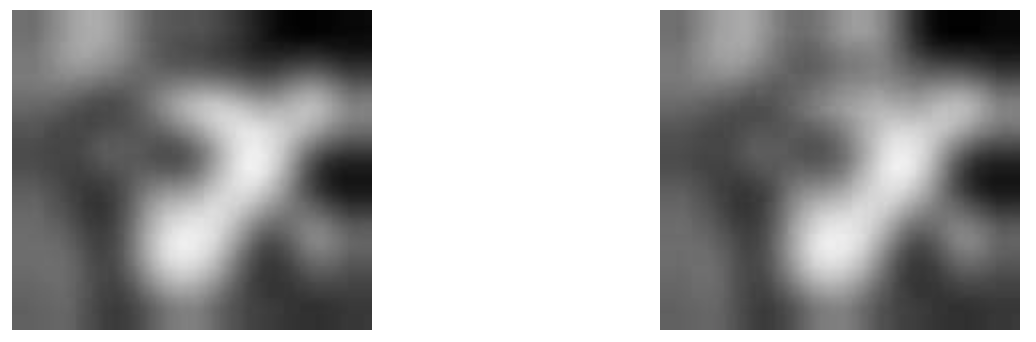
Not much of a difference now, eh?

Hashing: dhash

Now we have some scaled down pictures - but we need to transform this image data somehow into numeric values, suitable for fast comparison. Generating hashes comes to mind.

So, what hashing algorithm to choose? dhash, an algorithm which compares neighbor pixels if they get darker or lighter, seems so be very accurate and also fast.

To apply it, all our pixels (represented as "intensity values") from our shrinked, grayscaled images will be compared to their right neighbor, so some kind of gradient will be established:

• If the right neighbors is lighter (or the same), write a 0
• If the right neighbor is darker, write 1

You can see that in the first row, the pixel first lightens up (0), then stays the same (0) and the fourth pixel in row is darker than the third => 1.

After this, we will end up with 8*8 values (for hash length 8) from which we can build a hex-hash. For the two koalas we end up with the following hashes:

You see straight here that they look nearly the same, and for an algorithm it is easy to compare bitwise how much of a difference there really is:

0010111001110101110001011010001111000111110011010100110101001110
0010111001100111110001011010001111000111110011010100110101001110
___________x__x_________________________________________________
= 2 bits difference

So the difference of the two hashes is 2 out of 64 bits in total, which makes the second image 96.875% similar to the first one from this point of view :-)

I changed the dhash function (in comparison to the blog post mentioned above) here so that it displays exactly the given bits at the right position, which also simplifies the code.

00101110 | 2e
01110101 | 75
11000101 | c5
...

For example, as in the picture above the difference-map starts with 0010 1110, which is in hex "2e", so the hex strings are a adequate representation which can be immediatly reproduced by looking at the image. On a bitwise level this doesn't make any changes as long as all the hex strings are generated the same way.

Comparing koalas

As a sample, I compared some other koala images. Three are modifications from the original image: with an additional light source in the upper left corner, repainted as dots, a skew version, and one reference with a completely different koala.

They scored as follows, value 0 as absolute no difference between the images, in respect to the "original" koala image from the beginning:

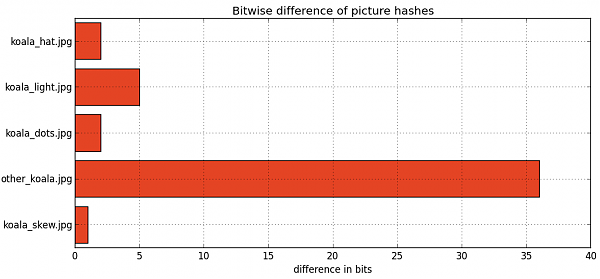
We see that the algorithm is robust against scaling or even to replotting with other techniques, and that the hash function is affected the most from lightning changes, for example re-highlighting the image with another light source. But even in this case the differences are reasonably small (5 bits difference).

Code

The code checks for all .jpg-images in the current working directory, picks the first one (in alphabetical order) and compares it to the others. Hashes are calculated with dhash, differences between hashes with diff, and then a horizontal bar plot is drawn with use of matplotlib.

Python Code (Python 2.7, using PIL and matplotlib/pylab and some koala images :-)

#!/usr/bin/python
# -*- coding: utf-8 -*-
'''Image comparison script with the help of PIL.'''
__author__  = "Adrianus Kleemans"
__date__    = "30.11.2014"

import os
import math, operator
from PIL import Image
import pylab

def diff(h1, h2):
    return sum([bin(int(a, 16) ^ int(b, 16)).count('1') for a, b in zip(h1, h2)])

def dhash(image, hash_size = 8):
    # scaling and grayscaling
    image = image.convert('L').resize((hash_size + 1, hash_size), Image.ANTIALIAS)
    pixels = list(image.getdata())

    # calculate differences
    diff_map = []
    for row in range(hash_size):
        for col in range(hash_size):
            diff_map.append(image.getpixel((col, row)) > image.getpixel((col + 1, row)))
    # build hex string
    return hex(sum(2**i*b for i, b in enumerate(reversed(diff_map))))[2:-1]

def main():
    # detect all pictures
    pictures = []
    os.chdir(".")
    for f in os.listdir("."):
        if f.endswith('.jpg'):
            pictures.append(f)

    # compare with first picture
    image1 = Image.open(pictures[0])
    h1 = dhash(image1)
    print 'Checking picture', pictures[0], '(hash:', h1, ')'

    data = []
    xlabels = []
    for j in range(1, len(pictures)):
        image2 = Image.open(pictures[j])
        h2 = dhash(image2)
        print 'Hash of', pictures[j], 'is', h2
        xlabels.append(pictures[j])
        data.append(diff(h1, h2))

    # plot results
    fig, ax = pylab.plt.subplots(facecolor='white')
    pos = pylab.arange(len(data))+.5

    ax.set_xlabel('difference in bits')
    ax.set_title('Bitwise difference of picture hashes')
    barlist = pylab.plt.barh(pos, data, align='center', color='#E44424')
    pylab.yticks(pos, xlabels)
    pylab.grid(True)
    pylab.plt.show()

if __name__ == '__main__':
    main()