kleemans.ch

For the last few years, I've been a regular customer at our local "Ludothek" (toy library), because it's just great to try out some new games for a while without buying them, especially with kids.

Last year I started helping out as a volunteer, and the biggest part of that is making sure that games which are returned are still complete (enough) to be borrowed to the next customer. For each game, there is an inventory list which states exactly what the game box is supposed to contain.

Now one of the more tedious things are jigsaw puzzles - sometimes you have to check 1000 pieces to see if a puzzle is complete or not. This is usually done by just counting the pieces individually:

Apparently there were already approaches with weighing (using a precision scale), but it turned out that the weight was fluctuating too much to make an accurate statement about the amount of pieces, probably because of differences in humidity. Between a week, the difference could be up to a gram or two, and as a single piece is often only around 0.5 grams, it would not be possible to detect a missing piece.

So I wondered, wouldn't it be possible to make a photo of pieces spread out across a uniform background and check with a script how many pieces were on the photo?

Getting started

To test the approach, I started out with a simple base image:

It has 72 pieces, which are all on their back, nicely spread apart.

My first idea was converting the image to greyscale and then applying a certain threshold, because the puzzle pieces have a different color than the background.

With OpenCV, an amazing image manipulation library, we have the necessary toolset to get started! (To install it, use pip3 install opencv-python).

import cv2

img = cv2.imread('test.jpg', cv2.IMREAD_GRAYSCALE)
threshold = 140
_, img_thresh = cv2.threshold(img, threshold, 255, cv2.THRESH_BINARY)
cv2.imwrite('test_thresh.jpg', img)

(Side note: The versions used in this post are opencv-python==4.11.0.86 and numpy==2.2.2).

Here are some examples for threshold of 110-140:

Clearly this will not work out, as the lighting is not uniform enough; Either the upper pieces start to merge with the light part, or the lower become part of the dark part, and there is no perfect threshold to capture them all.

Canny edges & contours

Just applying a threshold didn't work, so I thought it would be nice to do some kind of edge detection. Luckily, OpenCV has tons of built-in image processing algorithms, like the Canny edge detection, so let's try that.

import cv2

img = cv2.imread('test.jpg', cv2.IMREAD_GRAYSCALE)
canny = cv2.Canny(img, 20, 120)
cv2.imwrite('test_canny.jpg', canny)

Not bad! Unfortunately a similar problem arises, depending on the threshold some puzzle pieces will also have their shadow detected as an edge, and at the same time, the upper part of certain pieces are not detected as an edge:

Related to this, there is a built-in OpenCV contour detection, which detects curves of continuous points of the same color, similar to the edge detection.

import cv2
import numpy as np

img = cv2.imread('test.jpg')
img_grey = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
_, thresh_img = cv2.threshold(img_grey, 120, 255, cv2.THRESH_BINARY)
contours, hierarchy = cv2.findContours(thresh_img, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)

# Create an empty image for contours and draw
img_contours = np.zeros(img.shape)
cv2.drawContours(img_contours, contours, -1, (0, 255, 0), 3)
cv2.imwrite('test_contours.jpg', img_contours)

But as this is a similar approach, we also see the same problems as before.

K-Means Clustering

With the methods above, we keep getting stuck with artefacts, so we probably have to to a bit more of preprocessing on the image.

Using a method called K-Means Clustering, we can first reduce the image to the minimum we're interested in - puzzle pieces and background. I recommend reading through Understanding K-Means Clustering and Chapter 3. Color Quantization of the OpenCV docs.

Inspired by this StackOverflow answer, this code will apply k-means clustering for color quantization:

import cv2
import numpy as np

def kmeans_color_quantization(image, clusters=2, rounds=1):
    h, w = image.shape[:2]
    samples = np.zeros([h * w, 3], dtype=np.float32)
    count = 0
    for x in range(h):
        for y in range(w):
            samples[count] = image[x][y]
            count += 1

    compactness, labels, centers = cv2.kmeans(samples, clusters,None,(cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 10000, 0.0001), rounds, cv2.KMEANS_RANDOM_CENTERS)
    centers = np.uint8(centers)
    res = centers[labels.flatten()]
    return res.reshape(image.shape)

# Load image and perform kmeans
image = cv2.imread('test.jpg')
image_orig = image

# k-means color quantization
image = kmeans_color_quantization(image)
cv2.imwrite('test_kmeans.png', image)

# Threshold
image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
_, image = cv2.threshold(image, 0, 255, cv2.THRESH_BINARY + cv2.THRESH_OTSU)
cv2.imwrite('test_kmeans_threshold.png', image)

# Laplace
img_laplace2 = cv2.Laplacian(image, cv2.CV_8U, ksize=3)
cv2.imwrite('test_kmeans_laplace.png', img_laplace2)

# Contours
img_contours = np.zeros(image_orig.shape)
contours, hierarchy = cv2.findContours(image, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
cv2.drawContours(img_contours, contours, -1, (0, 255, 0), 3)
cv2.imwrite('test_kmeans_contours.png', img_contours)

Now if we run this code, we get an image which is reduced to 2 colors:

Amazing - exactly what we wanted! Now we can apply what we learned before and also draw images with threshold, contours and edges (this time using cv2.Laplacian, another helpful OpenCV function):

Now we can count the contours and be done, right? Let's check the output:

Total contours: 65

Hmmm... Something's not right - there are 72 puzzle pieces in the picture.

Inspecting contours

The problem: Some pieces seem to be connected and are counted as one contour:

What if we could check the amount of pixels each contour has, and then determine whether it's a single piece, two pieces, or even more connected pieces?

Now to work with the contour we have to make sure we know what we're doing with the cv2.findContours() call, so let's have a look at this line:

cv2.findContours(image, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)

There are 2 parameters:

• The RetrievalMode, which is set to cv2.RETR_EXTERNAL, meaning "retrieves only the extreme outer contours", which is already what we want. The other options would allow for nested / hierarchical objects, but this is not the case for us.
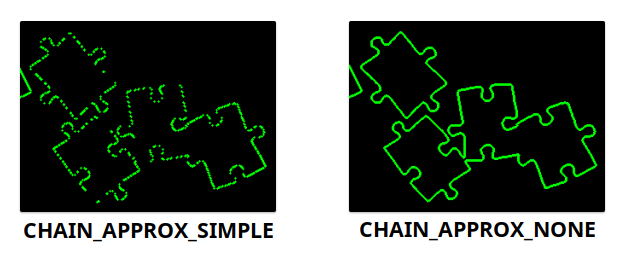
• The second parameter is the ContourApproximationMode, which defines how the contours will be stored. Up until now we used CHAIN_APPROX_SIMPLE, which compresses paths and and only leaves end points. Here it makes sense to switch to CHAIN_APPROX_NONE, so we get the full list of points, so we can easier check the circumference per contour.

Here's to illustrate the difference between the two modes:

Now that we have the pixels per contour, we can have a look at them:

All contour pixel counts: [255, 280, 287, 294, 294, 303, 303, 309, 309, 311, 312, 316, 319, 319, 320, 321, 321, 323, 323, 324, 327, 330, 331, 333, 335, 336, 337, 338, 338, 340, 341, 343, 347, 347, 350, 350, 351, 354, 355, 355, 355, 357, 359, 359, 361, 361, 365, 367, 369, 370, 377, 377, 379, 381, 381, 382, 388, 396, 398, 665, 666, 706, 755, 756, 1029]
Median: 347

Now if we take the median of 347 pixels and check for each value which multiple of the median is nearest (1 piece = 347 pixels, 2 pieces = 694 pieces, etc.), we can evaluate wether we're dealing with one, two or three pieces:

Applying this, we get the following output:

Total contours by median: 72

Hooray, it worked out!

Testing with other images

The approach worked with the example picture (which I spent some time in arranging the pieces), but will it also work for other constellations? Let's see!

• Background not uniform: Not working, k-means can't differentiate pieces from background.

• Pieces not all on their back: Not working.

The patterns of the puzzle motif interfere with the k-means clustering:

So for non-uniform backgrounds or if the pieces are not all on their back, unfortunately it doesn't work at all.

To finish it off, let's have a look at two more examples where it works fine.

65 pieces correctly recognized:

39 pieces correctly recognized:

Conclusion

Source code for counting & image generation: Gist

Even though it was fun digging into what is possible with OpenCV, for now I don't see a way to practically use it to count puzzles. The effort to get the pieces prepared so they can be processed (properly distributed out and turned to their back side) is just too high and might be almost as much as just counting them.

So for now, this is it :-) Maybe one day, I'll dig deeper into other approaches like Harris Corner detection in OpenCV (like done here for jigsaw puzzle pieces), or K component extraction, but for now....

Happy counting! :'-)