kleemans.ch

'Flocking', or how movement in swarms / herds / flocks is organized, is a fascinating behaviour to observe. As complex as it may be, using a few simple rules, it's possible to simulate a behaviour that gives really impressive results.

I wrote a flocking behaviour with inspiration and help from sources below. This is the full simulation (code on Github), powered by ProcessingJS:

Click left to place or remove an obstacle.

Click right to reveal bird #0 and its movement vector.

After reading this post about flocking I wanted to better understand Harry Brundage's implementation and write a simulation from scratch (but adapting some of his ideas, like the spreading from the center). Using only three simple rules, it should be possible to simulate a flocking behaviour in a realistic manner, with the result above.

The original algorithm

Craig Reynolds proposed the original flocking algorithm back in 1986 already and describes the following three forces (description on Wikipedia) involved:

• Alignment: Move in the same direction as your neighbours.
• Cohesion: Remain close to your neighbours.
• Separation: Avoid collisions with your neighbours.

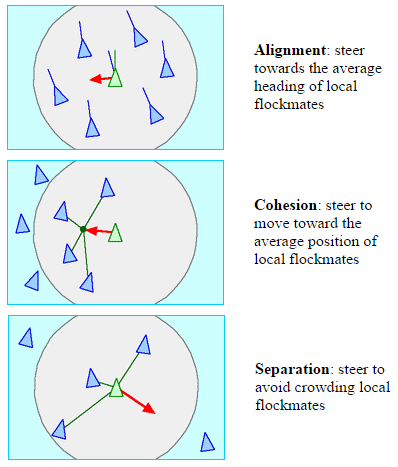
Images from Craig Reynolds' post

Alignment

For the alignment, we just look were the neighbours are heading (their speed vector) calculate the mean and limit that value by a MAX_FORCE constant.

alignment = new PVector(0, 0);
for (int i = 0; i < n.size(); i++) {
    alignment.add(n.get(i).speed); // add speed
}
if (n.size() > 0) alignment.div(n.size()); // mean speed vector
alignment.limit(MAX_FORCE);

Cohesion

Cohesion works in a similar way, only instead of the average speed, we calculate the "average position", the center of mass. Then we steer in that direction, by subtracting our own position:

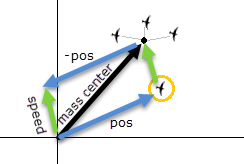
cohesion = new PVector(0, 0);
for (int i = 0; i < n.size(); i++) {
    cohesion.add(n.get(i).pos);  // add positions
}
if (n.size() > 0) {
    cohesion.div(n.size()); // center of mass
    cohesion.sub(pos); // cohesion - pos
    cohesion.limit(MAX_FORCE);
}

Separation

Separation was a bit trickier, because now only those neighbours wo come really close trigger a separation movement. The closer they come, the stronger the birds try to avoid a collision.

separation = new PVector(0, 0);
int count = 0;
for (int i = 0; i < n.size(); i++) {
    PVector neighbour_pos = n.get(i).pos;
    float d = PVector.dist(pos, neighbour_pos);
    if (d < DESIRED_SEPARATION) {
        PVector repulsion = pos.get();
        repulsion.sub(neighbour_pos);
        repulsion.normalize();
        repulsion.div(d);
        separation.add(repulsion);
        count += 1;
    }
}
if (count > 0) separation.div(count);

As with the cohesion, we work with the two positions ("our own" from the bird's view and the position of the neighbour) and calculate a direction vector, but only this time it points away from the other bird, so that our bird can escape. The vector then is normalized (recalculated to a vector with same direction but length 1) and divided by the distance between them. So if they're really close, the force to drift them apart becomes stronger and stronger.

Mouse obstacle

In addition it's possible to place an obstacle, by clicking left anywhere on the canvas:

The birds react similar to the separation rule, only that the radius of the obstacle is much bigger than those of a bird. The force is also directly proportional to how near it is to the center.

Balance

Setting all the parameters so that the system is balanced was quite tricky, and I ended up first setting the neighbour circle (a radius / distance in which a bird sees other birds as neigbhbours) and the separation circle.

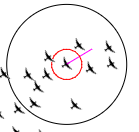
The neighbour circle (black) and the separation circle (red).

With different weights, it's important that they stay in balance. For example, when setting the cohesion too high, the birds would slow down (because they were all steering towards each other) and eventually come to a standstill. It's more important to fly in the same direction than steering to the mass center of the flock, so I set the weighs accordingly. Also, separation has to be quite strong, which is not a problem because the force is only active when the birds are really close.

float SEPARATION_WEIGHT = 1;
float ALIGNMENT_WEIGHT  = 0.4;
float COHESION_WEIGHT   = 0.2;

After 20-30s, the simulation above should stabilize and there should be some flocks:

You can find the whole code in this Github Repo.

Pitfalls

Javascript's Modulo - I've had some trouble with disappearing birds, when I let the simulation run some minutes the canvas would be empty after a while. Sometimes the birds would just disappear - but only if they flew upwards. When reaching the left, right or bottom boundary, they would be moved correctly to the opposite side. So I figured out this had to be something with ProcessingJS' modulo function (which is compiled into Javascript), which I used to make sure the birds wouldn't get outside the canvas. After some tests and pinning it down to the Modulo function indeed I stumbled upon this Stackoverflow post and the problem was easily fixed.

While some say it's a bug, technically the % in Javascript seems to be the the Remainder operator instead of just modulo. I fixed it by using my own modulo function.

function mod(n, m) {
    return ((n % m) + m) % m;
}

// move function - wrap around if out of canvas
void move() {
    pos.x = mod(pos.x + speed.x, w);
    pos.y = mod(pos.y + speed.y, h);
    ...
}

Angle between vectors - Another problem was the correct angle for drawing the bird image I'm using. For each bird on the canvas I had to take the angle they're moving at into account when drawing the picture and rotate it accordingly. ProcessingJS offers a function angleBetween(), but that just seems to calculate the shortest possible angle, which was not what I wanted, so I had to rewrite the function into strictly calculating the clockwise angle, starting from PVector a:

function calculateAngle(PVector a, PVector b) {
    float rot = PVector.angleBetween(a, b);
    if (b.y < 0) rot = 2*PI - rot;
    return rot;
}

Thanks for reading!