Huffman coding
Compression is an interesting task. How can we compress data - like text - so that it takes up less space, with the ability to fully restore the original data? (By the way, how to do that in the best way possible for a certain dataset is still an ongoing task, have a look at the Hutter Prize!)
A pretty good and widely used way is Huffman coding, which I'll be implementing in this post.
Assigning codes to characters
One important concept is to assign "codes" to the characters of a source text, and then optimize which character gets which code.
For example, ASCII itself is already a character to code assignment. If we have a source text of veni, vidi, vici, the ASCII codes are as follows:
v = 0111 0110
e = 0110 0101
n = 0110 1110
i = 0110 1001
, = 0010 1100
_ = 0010 0000
v = 0111 0110
i = 0110 1001
d = 0110 0100
i = 0110 1001
, = 0010 1100
_ = 0010 0000
v = 0111 0110
i = 0110 1001
c = 0110 0011
i = 0110 1001Every character takes up 8 bits, so the total message veni, vidi, vici takes up 16 * 8 = 128 bits.
But what if we use shorter codes? As we only have 8 different characters, we can just assign numbers from 1 to 8:
e = 000
c = 001
d = 010
i = 011
n = 100
v = 101
, = 110
_ = 111Now we only use 3 bits per character, totalling in 16 * 3 = 48 bits. But is it possible to improve this?
Huffman coding
The message above has the characters v and i multiple times. So maybe can we just assign shorter codes to those, but longer codes to characters which appear only once (like c and d)?
Also, the catch is that if we use a short code like 10 for a character, we can't use that sequence at the start of any other code, because then we wouldn't know how to decompress it if we encounter it in a compressed text.
That is exactly the motivation behind optimizing compression, and Huffman came up with a "theoretically optimal" method (for this class of methods).
The basic algorithm is pretty simple and goes like this:
- First, add a node for each character to a queue, with the weight as the frequency of appearance.
- While there is still more than one node in the queue:
- Remove the two lowest-weighted nodes and create a new one with the combined weight, setting the previous nodes as children
- Add the new node to the queue and re-sort the queue
- The last node is the root note.
Or, in code:
# Node class
class Node(object):
def __init__(self, idx, symbol, weight, child1=None, child2=None):
self.idx = idx
self.symbol = symbol
self.weight = weight
self.child1 = child1
self.child2 = child2
self.bits = ''
# Initialize nodes - data holds the message, chars contains all the different characters
nodes = []
idx = 0
for c in chars:
n = Node(str(idx), c, data.count(c))
idx += 1
nodes.append(n)
nodes.sort(key=lambda x: x.weight, reverse=True)
# Build tree
while len(nodes) > 1:
nodes.sort(key=lambda x: x.weight, reverse=True)
# Build new node
c = [nodes.pop(), nodes.pop()]
n = Node(str(idx), str(idx), c[0].weight + c[1].weight, c[0], c[1])
idx += 1
nodes.append(n)See here for a more in-depth explanation:
If we apply this to our message, we get the following encoding:
idx char count code
2 "i" 5 11
7 "v" 3 00
3 "," 2 011
6 "[sp]" 2 010
0 "e" 1 1001
1 "d" 1 1000
4 "c" 1 1011
5 "n" 1 1010The tree looks like this:
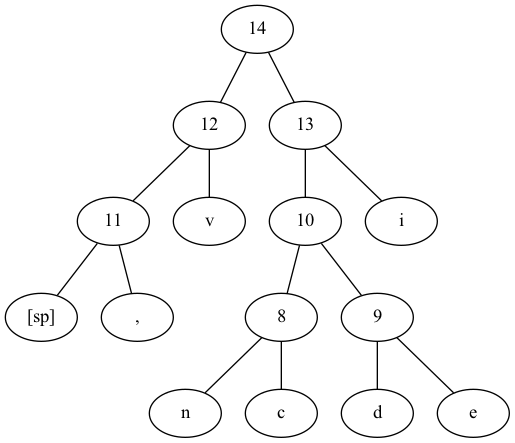
With this, we can compress our original message to 00100110111101101000111010110110100011100011 - only using 44 bits!
Applying it to more text
How does this work for bigger texts? If we take the complete works of William Shakespeare, the output is as follows:
id symbol count code
2 "[sp]" 169858 110
11 "e" 94611 1110
3 "t" 67009 1000
30 "o" 65798 0111
23 "a" 55507 0100
52 "h" 51310 0010
61 "s" 49696 0001
56 "r" 48889 0000
27 "n" 48529 11111
15 "i" 45537 10111
12 "[nl]" 40004 10100
33 "l" 33340 10010
40 "d" 31358 01100
48 "u" 26584 00110
29 "m" 22243 101101
42 "y" 20448 101011
5 "," 19843 100111
36 "w" 17585 100110
28 "f" 15770 011010
39 "c" 15622 010111
7 "g" 13356 001111
25 "I" 11832 1111010
6 "b" 11321 1111000
41 "p" 10808 1011001
13 ":" 10316 1011000
16 "." 7885 0110110
10 "A" 7819 0101101
44 "v" 7793 0101100
49 "k" 7088 0101001
24 "T" 7015 0101000
38 "'" 6187 11110111
31 "E" 6041 11110110
43 "O" 5481 11110010
37 "N" 5079 10101010
26 "R" 4869 10101001
50 "S" 4523 01101111
57 "L" 3876 01010111
4 "C" 3818 01010110
45 ";" 3628 01010100
46 "W" 3530 00111011
9 "U" 3313 00111001
34 "H" 3068 00111000
22 "M" 2840 111100110
21 "B" 2761 101010111
60 "?" 2462 101010110
51 "G" 2399 101010001
17 "!" 2172 011011101
47 "D" 2089 011011100
1 "-" 1897 010101011
18 "F" 1797 010101010
0 "Y" 1718 001110101
58 "P" 1641 001110100
59 "K" 1584 1111001111
14 "V" 798 11110011101
8 "j" 628 10101000011
35 "q" 609 10101000010
32 "x" 529 10101000000
55 "z" 356 111100111001
19 "J" 320 111100111000
53 "Q" 231 101010000010
54 "Z" 198 1010100000111
20 "X" 112 1010100000110Or, visualized, it looks like this:
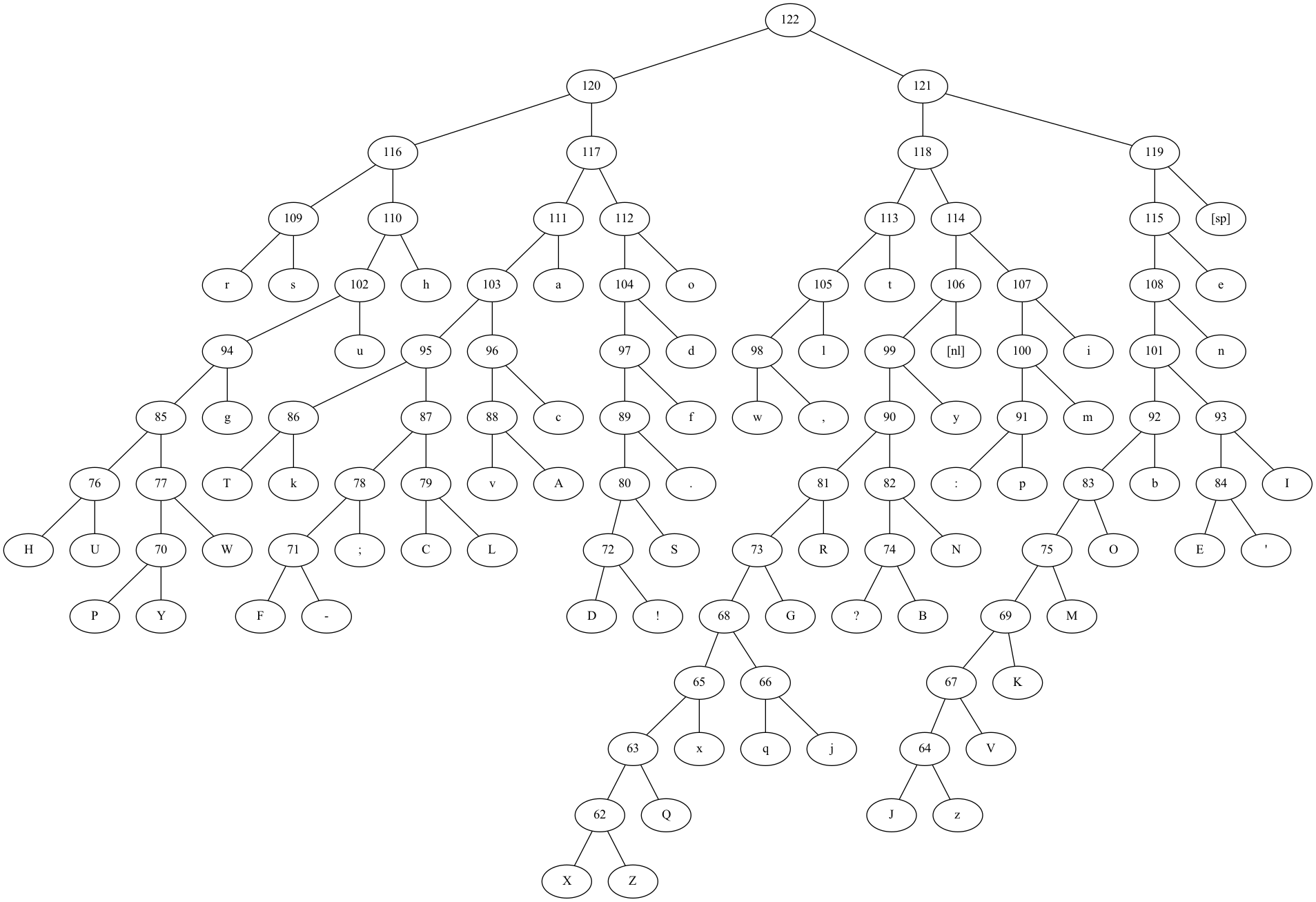
The compression ratio is as follows:
- Original file
shakespeare.txt: 1'115'328 bytes - Compressed file
shakespeare.bin: 671'524 bytes
So the compressed data is only 60.2% of the original data!
By the way, to decompress it, we can just run read through the bits and if we found a matching sequence, write it to an output:
_bytes = numpy.fromfile('compressed.bin', dtype="uint8")
bits = numpy.unpackbits(_bytes)
with open('decompressed.txt', 'w') as write_file:
buffer = ''
for bit in bits:
buffer += str(bit)
if buffer in nodes:
write_file.write(nodes[0].symbol)
buffer = ''For the graphs, pydot was used. All code can be found here.
Thanks for reading!