kleemans.ch

Static Pages

Search

Links

My bachelor thesis - cp-logic
November 29, 2020

Some time ago I finished my bachelor in computer science. It was about creating a toolbox in the field of classical propositional logic for trying out the concepts we were taught in the course. It looks like this (click for bigger image):

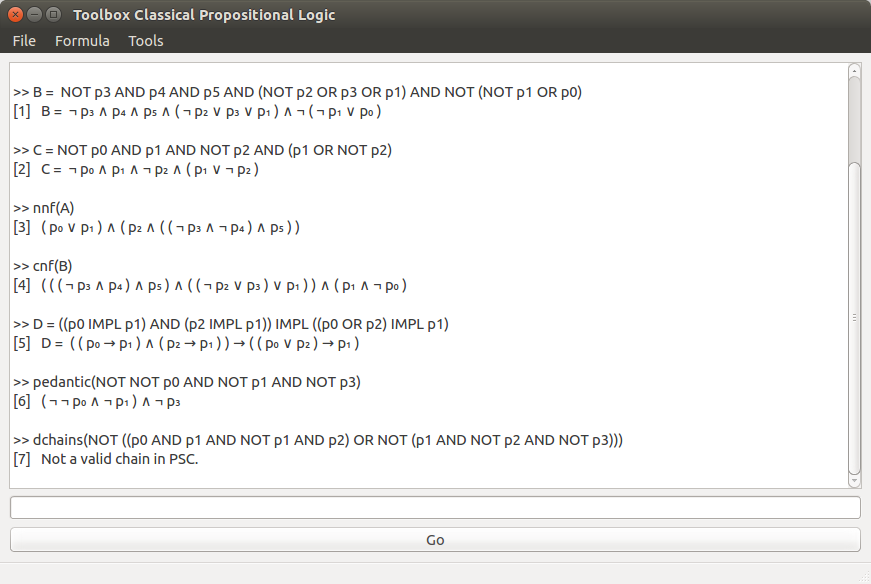
It does the following things:

You can find all the code in this Github repo, if you want to try it yourself! Most of it is written in Python and can be used via a GUI.

Working with formulas

Classical Propositional Logic can be represented by some basic symbols, for example p₀ (proposition), ∧ (AND), ∨ (OR), ¬ (NOT), → (implication), ⊤ (top), ⊥ (bottom) and () (brackets).

With these symbols, we can create statements (or propositions, hence the p), for example:

  • p₀: On wednesday, it rains.
  • p₁: Today is wednesday.
  • p₂: It rains today.

We can then link them together, which gets us more statemends:

  • p₁ ∨ p₂: Either today is wednesday, or it rains (possibly both).
  • ¬p₁: Today is not wednesday.
  • p₀ ∧ p₁ → p₂: If it rains on wednesdays and today is wednesday, it rains today.

The "statements" p₀, p₁ can be either true or false, and playing around allows us to check if the whole statements can be true. All those statements can again be true or false themselves, so you can build pretty complex stuff.

So back to the tool, you can type in formulas:

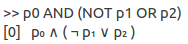
As you see, keywords like AND and NOT are automatically converted into symbol form.

You can also save them into a newly created "metavariable", for example A:

From now on you can use A, for example in other formulas, just as you would with "plain" proposition variables. We can also apply functions to formulas, just as in other languages with the function name and bracket.

I found this quite interesting, because internally the program had to know which parts would belong together and in what way a formula would be evaluated, so I worked with a depth concept, to better visualize the "inner structure" of a formula.

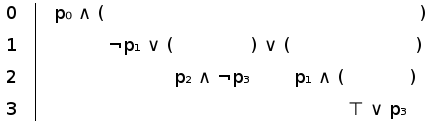
For example, if we want to check what is included in the "AND"-clause, we need to know where it ends:

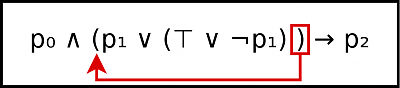
With the depth concept - and knowing on which "level" you are anywhere in the formula - was helpful to tackle such things.

Using functions

Finding parts of a formula was important for converting them into different normal forms, like the Negation normal form (NNF). This meant that implications (→) had to be converted, like this:

There are also helper functions like getting all subformulas (sufo()) or for example the length of a formula (number of symbols):

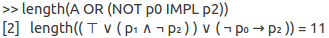
Cool things is that they can also be nested, where it makes sense, sou you could write

sufo(nnf(p0 OR NOT p1))

which would give you all subformulas (of all depth levels, see above) of the NNF of the formula.

Satifiability

To check for basic satisfiability (if there is a proposition combination which makes the whole statement true), we can use the function sat(A) (with our metavariable A from above, A = ⊤ ∨ (p₁ ∧ ¬p₂)):

This means that our formula A can resolve to true with both p₀ and p₁ being false. In fact, as A begins with ⊤ (the true "literal"), anything that follows doesn't really matter and so the first combination (both p's being false) will be returned.

This should work without problems with up to 10 variables, with more it gets really slow, because the algorithm is a really simple inefficient brute-force search until it hits a valid result.

Deduction chains

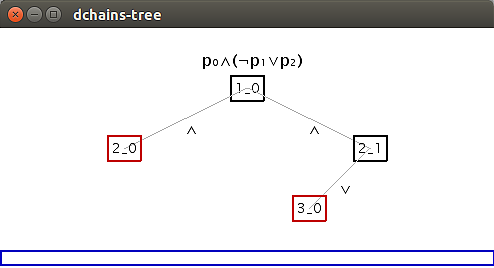
With formulas in normal form (with only propositions and ∧ / ∨ connecting them), you can also show them as a graph, where each node is a proposition, and they are connected with either AND or OR:

For more complex formulas this looks quite fancy:

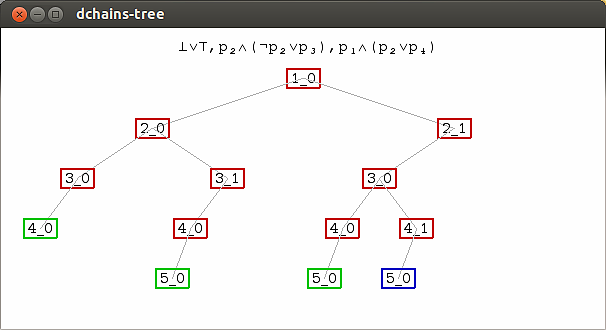
The colors mean whether the node is to be always true (or an "axiom of PSC", green) whether it is still further reducible (not a leaf node, blue) or others (red). See this this script for further reading on deduction chains.

Testing and exception handling

Testing was also a big part of the project. Most important was the Formula class, many tests are specifically for testing all kind of formula inputs and functions, for example:

I also made some custom exceptions, to better categorize what could go wrong and react to it. For example the FormulaInvalidError, to check formulas on user input:

  • Invalid symbols: p₀a
  • Propositions without index: p
  • Missing connection between propositions: p₀ p₁
  • Mixed AND or OR on same level (ambiguity): p₀ ∨ p₁ ∧ p₂
  • Invalid negation (p₀ ∨ ¬), invalid connections (p₀ ∨ ∧ p₁), invalid implications (p₀ → p₁ → p₂), invalid brackets ((p₀ ∨ p₁))), etc.

Having many tests helped me a lot solving many problems before I even started to work with formulas, so I had a really good foundation of validated formulas before moving on to the fancier things. Often I worked test-driven and would write the test first, also because it was really easy with the Python unittest module.

You can find everything in the Github repo. Here some quick links to:

Thanks for reading ∧ happy coding!