kleemans.ch

Passend zur laufenden WM werden wieder Panini-Hefte angeboten, und wie jedes Mal sind die hohen Kosten für die Klebebildchen ein Thema. Im Artikel auf Spiegel Online ist schön erklärt, wie sich berechnen lässt, wie viel Panini-Bilder gekauft werden müssen, bis man ein Heft voll hat. Es geht dabei rein darum, wie viel man kaufen müsste, ohne zu tauschen oder Bilder beim Hersteller zu bestellen.

Berechnung

Einfach gesagt geht es um die Wahrscheinlichkeit, dass ein neu gekauftes Bild noch nicht in der Sammlung vorhanden ist. Ich gehe von der Schweizer Version aus, in der nebst den 640 im Heft auch die 20 Kleber im Poster geholt werden müssen, also 660 insgesamt. Weiter gehe ich von einer Gleichverteilung der Bilder aus (was in Deutschland offenbar nicht selbstverständlich ist).

Beim ersten Bild ist diese 660/660, also 100%, da es das erste Bild ist. Beim zweiten Bild ist es 659/660, also etwa 99.85%, und so weiter, bis man beim letzten Bild noch eine Wahrscheinlichkeit von 1/660 hat (~0.15%), das Richtige, also letzte Fehlende zu erwischen.

Diese Wahrscheinlichkeit kann man nun anders formulieren, nämlich als Frage: Wie viele Bilder muss ich kaufen, bis ich das nächste fehlende Bild erhalte? Dazu kehrt man die Wahrscheinlichkeit um. Beim ersten sind dies 660/660, also 1. Wenn ich zum Beispiel die Hälfte aller Bilder habe, also 330, dann muss ich im Schnitt 660/330, also 2 Bilder kaufen, bis ich eines erhalte was mir noch fehlt. Beim letzten sind dies ganze 660/1 = 660, da ja nur noch eines von 660 fehlt.

Summiert man nun all diese Zahlen zusammen (660/660 + 660/659 + 660/658 + ... + 660/1), kommt man auf 4666.34, also die Zahl an Bildern, die es braucht, um ein volles Heft zu erhalten.

Das Modell ist aber nicht ganz korrekt, da ja immer Päckchen von 5 gekauft werden, die in sich nie Doppelte Bilder enthalten.

Simulation

Doch wie sieht es nun aus wenn 5 Päckchen gekauft werden? In einer einfachen Simulation, in der schrittweise Päckchen à 5 Bilder gekauft werden, also wie im realen Leben, wird simuliert, wie lange es dauert, bis auch das letzte Bildchen in der Sammlung vorhanden ist (Quellcode ganz unten).

• Um 50% der Bilder zu besitzen, müssten im Schnitt 91 Päckchen (455 Bilder) gekauft werden
• Für 75% braucht es insgesamt 182 Päckchen (910 Bilder)
• Um 90% der Bilder zu besitzen, müssten schon 301 Päckchen gekauft werden (1505 Bilder).

Um 100%, also alle Bildchen zu erhalten, musste ich die Simulation etwas anpassen, da aufgrund der grossen Abweichung die Resultat bei nur 100 Durchläufen zu wenig genau waren. Lässt man die Simulation aber mit z.B. einer Million Durchläufen arbeiten, dann kommt man auf folgende Zahlen: Für ein volles Heft müssten ganze 930 Päckchen gekauft werden. Dann hat man insgesamt 4650 Bilder.

Hier noch als Grafik über alle Prozentsätze und Anzahl Päckchen, die man kaufen müsste:

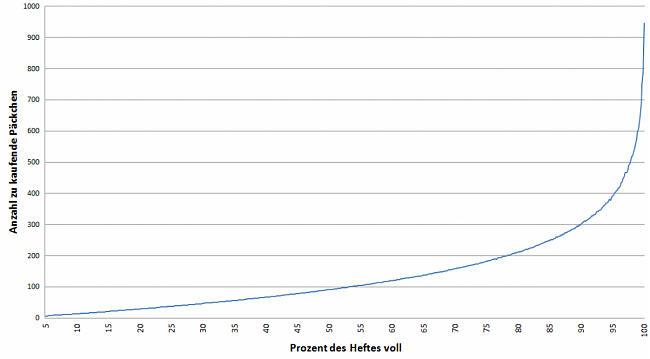
Der Anstieg am Schluss fällt besonders ins Auge. Es lohnt sich also schon relativ bald einmal, mit dem Tauschen anzufangen.

Interessant ist auch, wie sich die Simulation (Durchschnitt der Anzahl gekaufter Päckchen für ein volles Heft) langsam auf einen bestimmten Wert einpendelt:

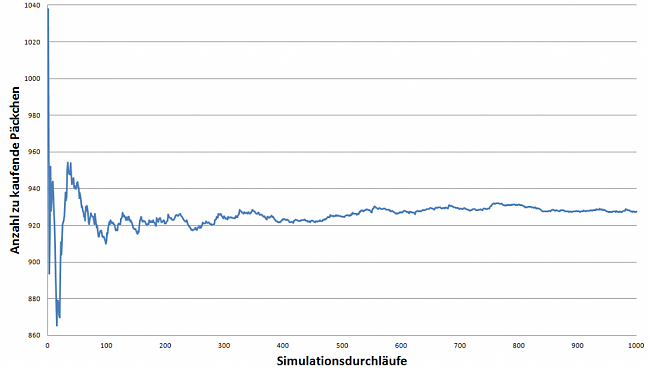
Zu Beginn sind die Zahlen noch weit auseinander (je nachdem wieviel "Glück" man haben würde beim Kauf), der Durchschnitt pendelt sich jedoch nach schon einigen hundert Durchläufen ein. (Die Berechnung kann man übrigens auch exakt durchführen, wie auf Wikipedia beschrieben - Sammlerbildproblem).

Fazit

Dadurch, dass innerhalb eines Päckchens keine doppelten Bilder vorkommen, muss man insgesamt gut 16 Bilder weniger kaufen, also kaum ein Unterschied (nur ~0.34% weniger!) zu der Version, in der die Bilder einzeln gekauft werden. Die Regelung scheint mehr einen praktischen Nutzen zu haben, oder ein Kniff vom Marketing des Herstellers zu sein :-)

Source Code: Der Code zur Berechnung (panini.py) findest du hier